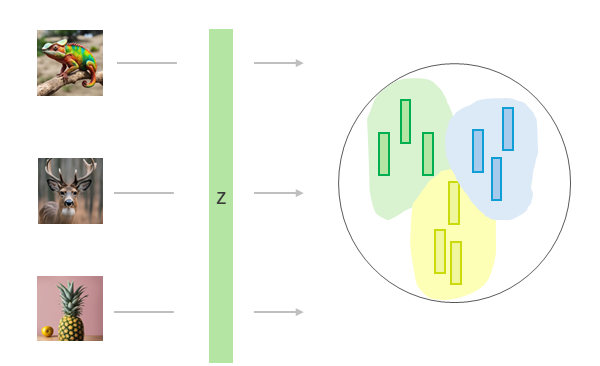
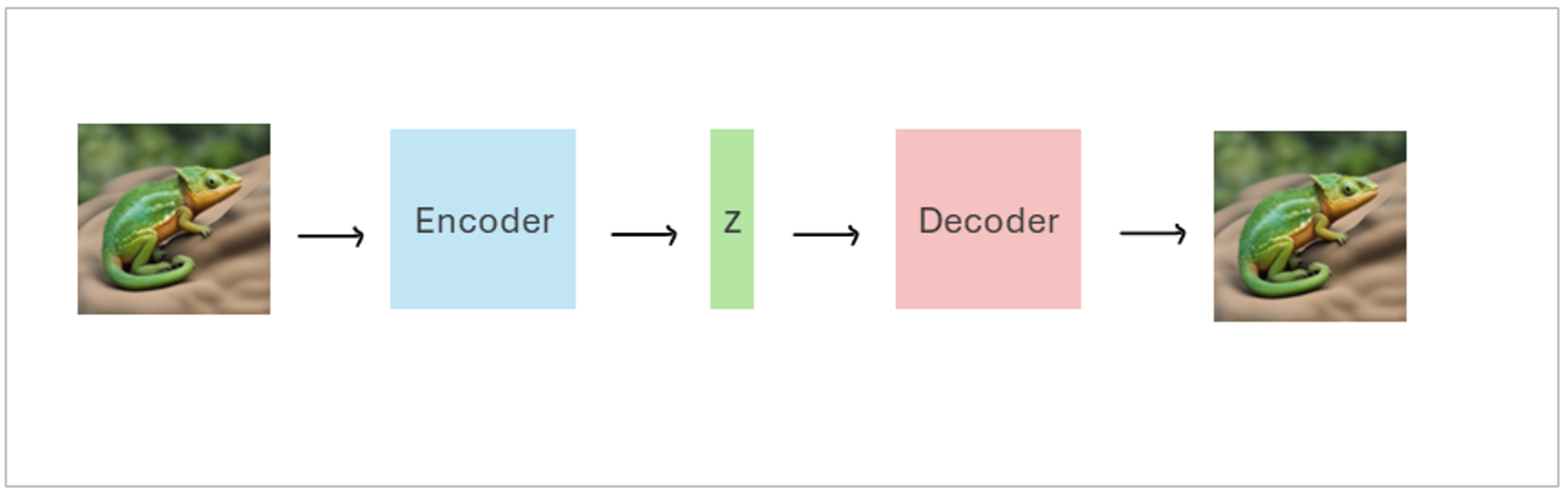
Variational Autoencoders are a type of generative model, designed to learn a representation of data and generate new data points similar to the original data.
They are built upon the architecture of traditional autoencoders, consisting of two main parts: the Encoder and the Decoder.
Architecture of Autoencoders
- Encoder: The encoder compresses the input data into a latent vector (a lower-dimensional representation).
- Decoder: The decoder takes this latent vector and reconstructs the original input data from it.
Small note: Despite the decoder being responsible for generating the output, the encoder plays a crucial role in producing a meaningful latent vector. If the latent vector is not well-structured, the decoder will generate meaningless outputs.
Variational Autoencoder vs. Autoencoder
The primary distinction between an Autoencoder (AE) and a Variational Autoencoder (VAE) lies in how the latent space is structured:
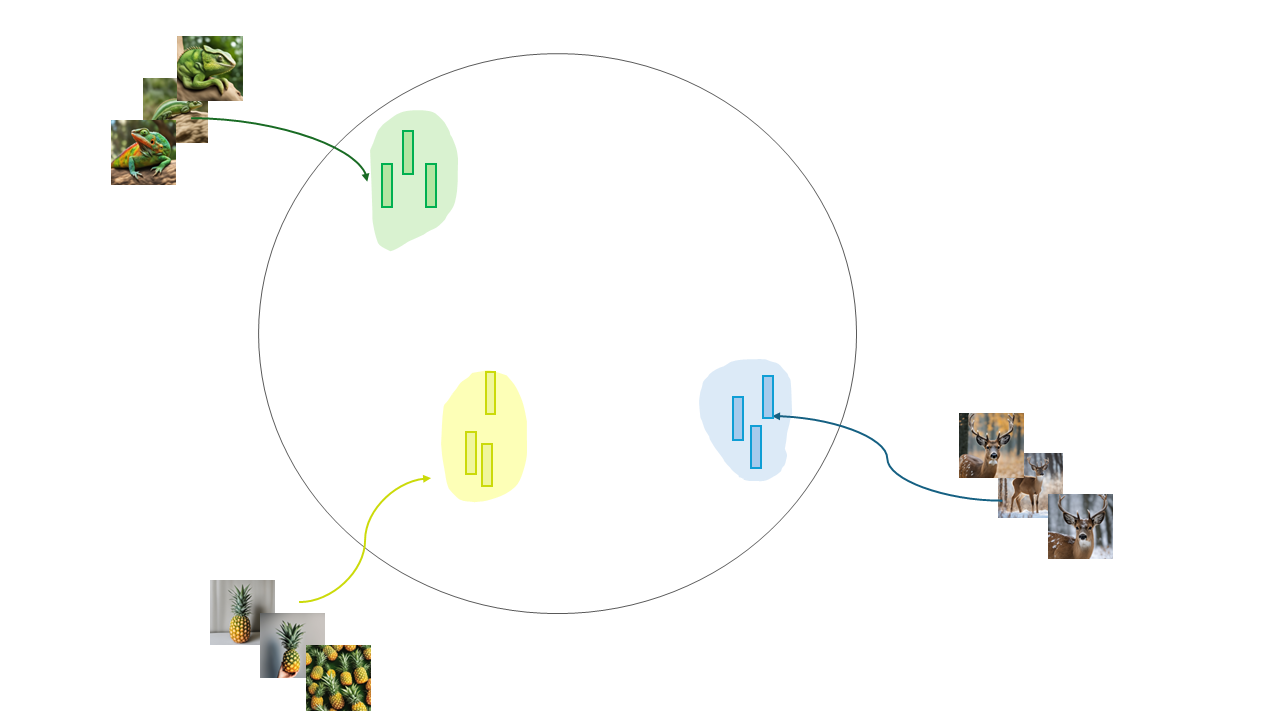
- Autoencoder (AE): An AE simply learns to map inputs to latent vectors and then back to outputs without any constraints on the latent space just like NN without any regularization. The embeddings of inputs can be very far apart from each other or not. This can lead to a disorganized latent space, making generation of new data challenging.
The embeddings of training inputs are learned during training. Without regularizing the space of the embeddings we might end up with a huge space with limited information.
During test time, we might end up with embeddings where we don’t have information in this big space.
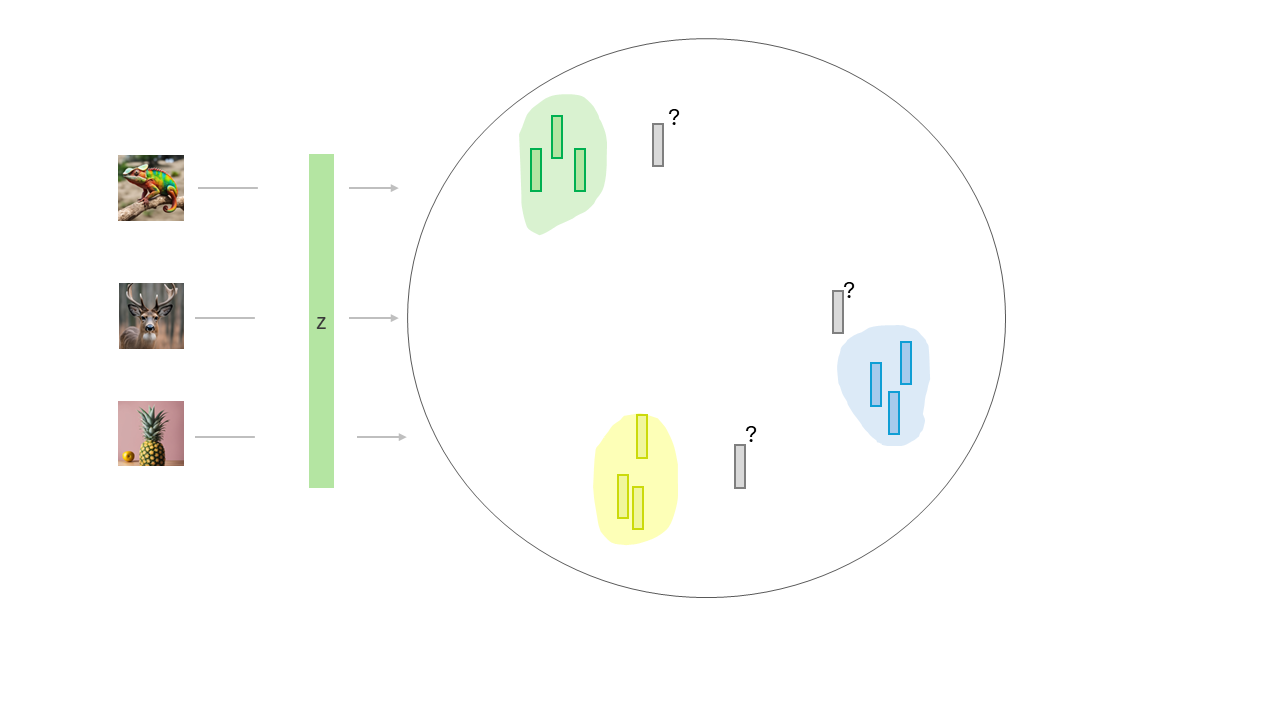
And.. During the test time in the decoding part, we might end up with meaningless outputs.
- Variational Autoencoder (VAE): A VAE imposes a structure on the latent space through regularization. Specifically, it constrains the latent vectors to follow a normal distribution N(0,I). This is achieved by introducing a latent loss (often referred to as the Kullback-Leibler divergence) during training, which forces the latent vectors to conform to this distribution.
A very high level representation for loss of the VAE:
Loss = Reconstruction Loss + Latent Loss
A very high level representation for loss for the AE:
Loss = Reconstruction Loss
Why Regularization is Necessary
The regularization in VAEs serves several purposes:
- Controlled Latent Space: By regularizing the latent space, the VAE ensures that similar inputs have similar latent representations. This structured latent space allows for more meaningful and coherent generation of new data.
- Generalization: During training, the VAE learns to map inputs to a specific, controlled space. As a result, when given new, unseen inputs, the VAE can project these inputs into this learned space and produce meaningful outputs. Without regularization (as in AEs), the latent vectors could be scattered randomly, leading to meaningless outputs for new inputs.
This regularization will actually force that the coming embedding from test input will be placed within this constrained space with this way the decoder part hopefully will be able to generate more meaningful outputs.